450-删除二叉搜索树中的节点

Doublew2w大约 4 分钟

给定一个二叉搜索树的根节点 root 和一个值 key ，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

示例 1:

  输入： root = [5,3,6,2,4, null,7], key = 3
 输出： [5,4,6,2, null, null,7]
 解释： 给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2, null, null,7], 如下图所示。
另一个正确答案是 [5,2,6, null,4, null,7]。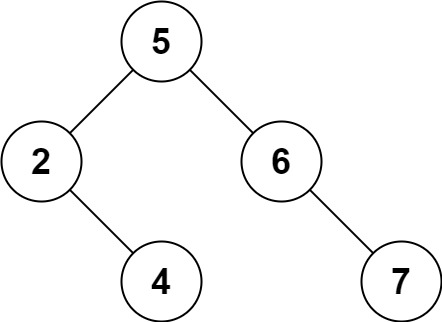

示例 2:

  输入:  root = [5,3,6,2,4, null,7], key = 0
 输出:  [5,3,6,2,4, null,7]
 解释:  二叉树不包含值为 0 的节点

示例 3:

  输入:  root = [], key = 0
 输出:  []

提示:

节点数的范围 [0, 10 ⁴] .
-10 ⁵ <= Node.val <= 10 ⁵
节点值唯一
root 是合法的二叉搜索树
-10 ⁵ <= key <= 10 ⁵

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

思路

以 root 为根的树，删除 key 的节点，并返回删除节点后的树。

public TreeNode deleteNode(TreeNode root, int key)

讨论几种情况：

当 root 为空（可能起始传入的 root 为空，也可能是递归过程中没有找到值为 key 的节点时，导致的 root 为空），我们无须进行任何删除，直接返回 null 即可
当找到对应的 key 节点后，讨论 key 节点情况
1. key 节点是叶子节点，那么就直接删除。删除后该节点位置就是 null。也就是返回 null，给上一层进行接收。
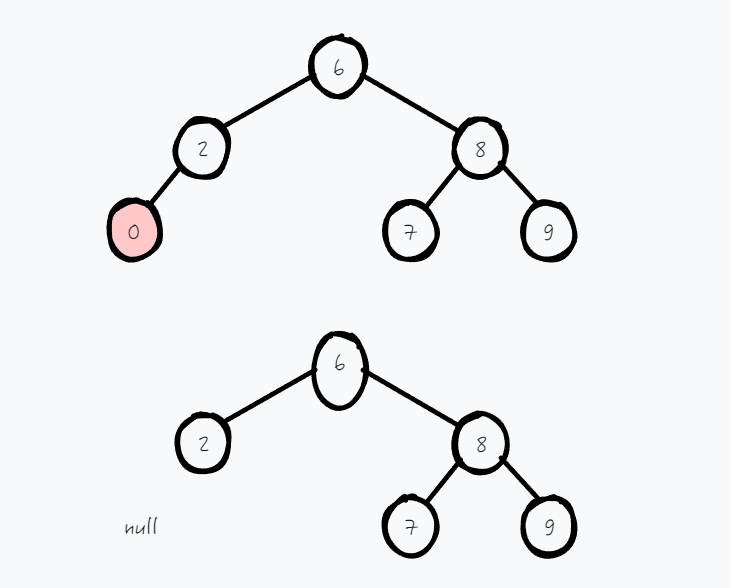
2. 若 key 节点的左子树为空，右子树不为空（左子树不为空，右子树为空），就直接返回右子树（左子树）
  因为这样子就可以将不为空的子树搬到上一层递归中 root 节点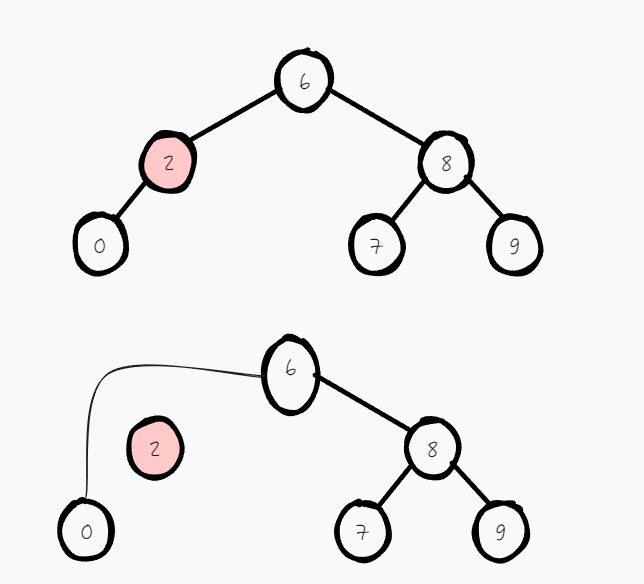
3. 若 key 节点的左右子树不为空
  1. 从「当前节点的左子树」中选择「值最大」的节点替代 root 位置
  2. 从「当前节点的右子树」中选择「值最小」节点替代 root 位置
  以从「当前节点的右子树」中选择「值最小」节点为例子，通过树的遍历。找到右子树中的最小值 10，假设是 t，肯定有 t.left ==null 。因为这个最小值都比「当前节点的左子树」的任何一个节点都大。所以直接将「当前节点的左子树」直接搬到「t 节点」的左子树也是符合 BST 特性的。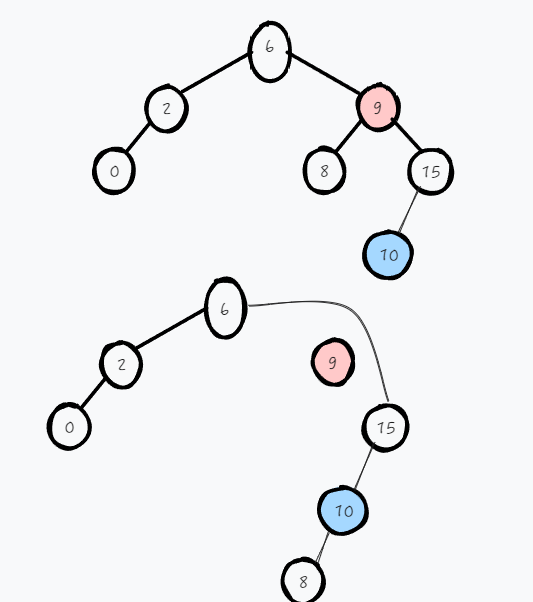
如果 root.val < key ，说明待删除的节点必然 不是当前节点，以及 不在当前节点的左子树中，我们将删除动作「递归」到当前节点的右子树, 并将删除（可能进行）之后的新的右子树根节点，重新赋值给 root.right。所以有 root.right = deleteNode(root.right,key)
如果 root.val > key，说明待删除的节点必然 不是当前节点，以及 不在当前节点的右子树中，我们将删除动作「递归」到当前节点的 右子树, 并将删除（可能进行）之后的新的右子树根节点，重新赋值给 root.left。所以有 root.left= deleteNode(root.left,key)

关键点

key 节点的情况讨论，以及结构的变化

代码

语言支持：Java

Java Code:


/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        // 终止条件
        if(root == null) return null;
        // 如果找到删除的节点
        if(root.val == key){
            if(root.left == null && root.right==null){
                // 如果是叶子节点，直接删除
                // 将 null 返回给上一层
                return null;
            } else if(root.left != null && root.right == null){
                // 如果是左不空右为空
                // 删除 root，将 root.left 返回给 root 的父节点
                return root.left;
            }else if(root.left == null && root.right != null){
                // 如果左空右不空
                return root.right;
            }else if(root.left != null && root.right != null){
                // 找到右子树的最小节点，并将左子树放到该节点的左子树上
                TreeNode cur = root.right;
                while(cur.left != null) cur = cur.left;
                cur.left = root.left;
                return root.right;
            }
        }
        if(root.val < key) root.right = deleteNode(root.right,key);
        if(root.val > key) root.left = deleteNode(root.left,key);
        return root;
    }
}

复杂度分析

令 n 为二叉树节点个数。

时间复杂度： $O(n)$ ，最差情况下，寻找和删除各需要遍历一次树。
空间复杂度： $O(n)$ ，递归的深度最深为 O(n)。

450-删除二叉搜索树中的节点

题目地址(450. 删除二叉搜索树中的节点 - 力扣（LeetCode）)

题目描述

思路

关键点

代码