226-翻转二叉树

Doublew2w大约 3 分钟

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

  输入： root = [4,2,7,1,3,6,9]
 输出： [4,7,2,9,6,3,1]

示例 2：

  输入： root = [2,1,3]
 输出： [2,3,1]

示例 3：

  输入： root = []
 输出： []

提示：

树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

## 思路 1：递归

所谓的翻转就是将二叉树上的每个节点的「左右子节点交换」

递归函数定义：

终止条件：当节点 root 为空时，直接返回 null;
单层递归逻辑：
1. 暂存节点 root 的左子节点（因为左子节点在翻转后会发生变化）
2. 递归翻转 root 的右子节点，递归的结果就是 root 的新左子节点
3. 递归翻转 root 的左子节点（旧），递归的结果就是 root 的新右子节点
返回值： root

关键点

翻转二叉树是改变树，而不是单纯的输出树节点，所以不能通过「层序遍历」方法输出
在翻转后子节点会发生变化。不要用

代码


/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        // 1. 终止条件：当节点为空时，返回 null
        // 2. 参数及返回值：root，root
        // 3. 单层递归逻辑：交换左右子树
        if(root ==null) return root;
        TreeNode temp = root.left;
        root.left = invertTree(root.right); // 处理右子树后，就是根节点的左子树（左子树已经发生变化）
        root.right = invertTree(temp); // 处理左子树，处理后变成根节点的右子树（不能使用 root.left）
        return root;
    }
}

复杂度分析

令 n 为二叉树节点个数。

时间复杂度： $O(n)$ ，需要遍历树的所有节点
空间复杂度： $O(n)$ ，最差情况下，二叉树退化为链表，需要开辟 $O(n)$ 的栈空间来递归

思路 2：层序遍历

使用一个队列存储每一层的遍历结果，并交换节点的左右子节点

提前将 root 节点入队
循环遍历，当队列为空时，退出循环
1. 出队节点 node
2. 将 node 的左右节点进行入队
3. 交换 node 的左右子节点

第一次循环后的情况如下：

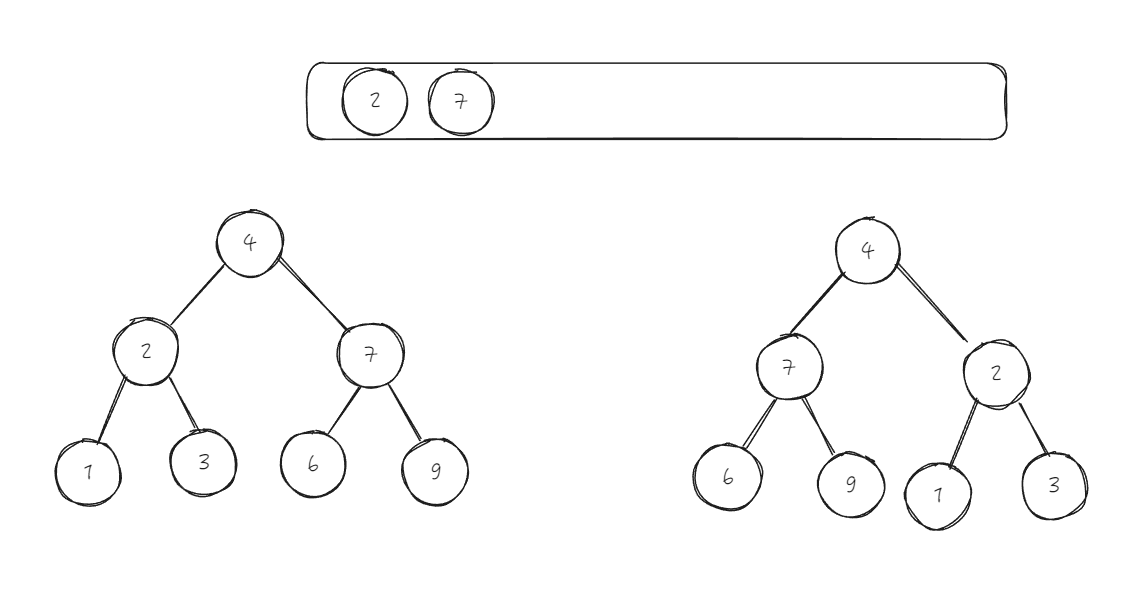
代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        // 层序遍历
        if(root == null) return root;
        Deque<TreeNode> deque = new ArrayDeque<>();
        deque.offerLast(root);
        while(!deque.isEmpty()){
            TreeNode node = deque.pollFirst();
            if(node.left != null){
                deque.offerLast(node.left);
            }
            if(node.right != null){
                deque.offerLast(node.right);
            }
            swapLeftRight(node);
        }
        return root;
    }

    public void swapLeftRight(TreeNode root){
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
    }
}

复杂度分析

令 n 为二叉树节点个数。

时间复杂度： $O(n)$ ，需要遍历树的所有节点
空间复杂度： $O(n)$ ，最差情况下，队列最多同时存储 $(N+1)/2$ 个节点，占用 $O(N)$ 额外空间。

226-翻转二叉树

题目地址(226. 翻转二叉树 - 力扣（LeetCode）)

题目描述

关键点

代码

思路 2：层序遍历

代码