101-对称二叉树

题目地址(101. 对称二叉树 - 力扣（LeetCode）)

https://leetcode.cn/problems/symmetric-tree/description/

题目描述

给你一个二叉树的根节点 root ， 检查它是否轴对称。

 

示例 1：

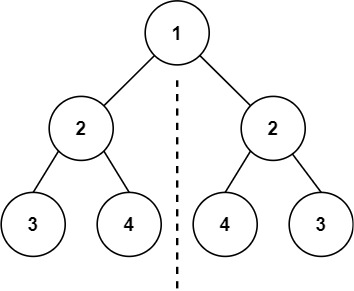
  输入： root = [1,2,2,3,4,4,3]
 输出： true

示例 2：

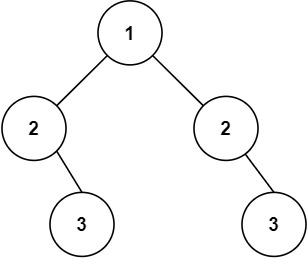
  输入： root = [1,2,2, null,3, null,3]
 输出： false

 

提示：

• 树中节点数目在范围 [1, 1000] 内
• -100 <= Node.val <= 100

 

进阶： 你可以运用递归和迭代两种方法解决这个问题吗？

思路 1：递归

定义递归函数：

1. 参数与返回值：入参是左子节点与右子节点，返回值是对称标志
2. 单层递归逻辑：
   1. 如果节点值不同，则为 false
   2. 如果其中一个为空，则为 false
   3. 如果都为空，则为 true
   4. 判断两节点 left.left 和 right.right 是否对称
   5. 判断两节点 left.right 和 right.left 是否对称
3. 终止条件：

关键点

两个二叉树互为镜像的定义：

• 两个二叉树的根节点的值相等

• 每个二叉树的右子树与另一个树的左子树互为镜像

如果以节点来说明：

• 两对称节点值相同：left.val = right.val
• left 的左子节点与 right 的右子节点相同：left.left.val = right.right.val
• left 的右子节点与 right 的左子节点相同：left.right.val = right.left.val

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
      return root == null || recur(root.left, root.right);
    }

    public boolean recur(TreeNode left, TreeNode right){
        if(left == null && right == null) return true;
        if(left == null || right == null || left.val != right.val) return false;
        return recur(left.left,right.right) && recur(left.right,right.left);
    }
}

复杂度分析

令 n 为二叉树节点个数。

• 时间复杂度：$O(n)$，每次判断一对节点是否对称，需要递归一次。
• 空间复杂度：$O(n)$，最差情况，二叉树退化为链表，共有 2n-1 个

思路 2：迭代

将递归逻辑写成迭代的形式。

将这个二叉树看成是两个 u，v，使用队列存储遍历过程中的每一对节点

• 对于根节点而已，入队两次，相当于处理这一对节点
• 对于其他的一对节点
  • 入队 u.left 和 v.right
  • 入队 u.right 和 v.left

代码

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return check(root, root);
    }

    public boolean check(TreeNode u, TreeNode v) {
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.offer(u);
        q.offer(v);
        while (!q.isEmpty()) {
            u = q.poll();
            v = q.poll();
            if (u == null && v == null) {
                continue;
            }
            if ((u == null || v == null) || (u.val != v.val)) {
                return false;
            }
			//1
            q.offer(u.left);
            q.offer(v.right);
			//2
            q.offer(u.right);
            q.offer(v.left);
        }
        return true;
    }
}

复杂度分析

令 n 为二叉树节点个数。

• 时间复杂度：$O(n)$，每次判断一对节点是否对称，需要递归一次。
• 空间复杂度：$O(n)$，使用一个队列维护节点，每个几点最多进队一次，队列中最多不会超过 n 个节点。