各种排序算法
大约 9 分钟
总览
稳定排序: 若两个元素相等:a = b,排序前 a 排在 b 前面,排序后 a 仍然在 b 后面,称为稳定排序。
不稳定排序: 若两个元素相等:a = b,排序前 a 排在 b 前面,排序后 a 有可能出现在 b 后面,称为不稳定排序。
| 名称 | 时间复杂度 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(1) | 内部排序 | 稳定 |
| 选择排序 | O(n^2) | O(1) | 内部排序 | 不稳定 |
| 插入排序 | O(n^2) | O(1) | 内部排序 | 稳定 |
| 希尔排序 | O(nlogn) | O(n) | 内部排序 | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | 外部排序 | 稳定 |
| 快速排序 | O(nlogn) | O(nlogn) | 内部排序 | 不稳定 |
| 堆排序 | O(nlogn) | O(1) | 内部排序 | 不稳定 |
| 计数排序 | O(n+m) | O(m) | 外部排序 | 稳定 |
| 桶排序 | O(n+m) | O(n+m) | 外部排序 | 稳定 |
| 基数排序 | O(n+m) | O(n+m) | 外部排序 | 稳定 |
冒泡排序
概念及演示
步骤解析:
将相邻的两个元素 a, b 进行比较,如果 a 比 b 大,那么就交换 a 和 b 的位置。当第一轮遍历结束后,最后一个元素就是最大的元素。
重复上一个过程,找出第 n 大的元素,直到剩下一个数字。
代码模板
public void bubbleSort(int[] array) {
if (array == null || array.length == 0) {
return;
}
int n = array.length;
boolean swapped;
for (int i = 0; i < n - 1; i++) {
swapped = false;
for (int j = 0; j < n - i - 1; j++) {
if (array[j] > array[j + 1]) {
// 交换 array [j] 和 array [j + 1]
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
swapped = true;
}
}
// 如果在这一轮排序中没有交换过,说明数组已经有序,可以提前结束
if (!swapped) {
break;
}
}
}- 在数据内部进行排序,无需额外的存储空间
- 当数组正序时,执行效率最高。当数组倒序时,执行效率最低,每次都要进行交换。
选择排序
概念及演示
每次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
- 把第一个没有排序过的元素设置为最小值
- 遍历后续的元素
- 如果元素 < 「现在的最小值」,则将元素设置为「新的最小值」
- 将最小值和第一个没有排序的元素进行交换
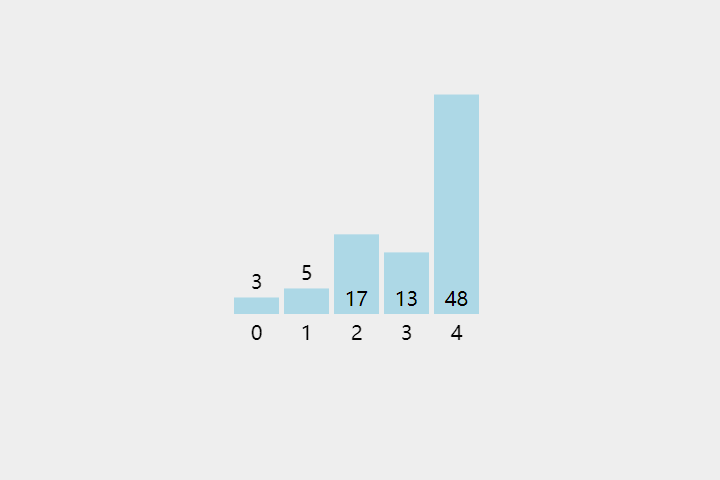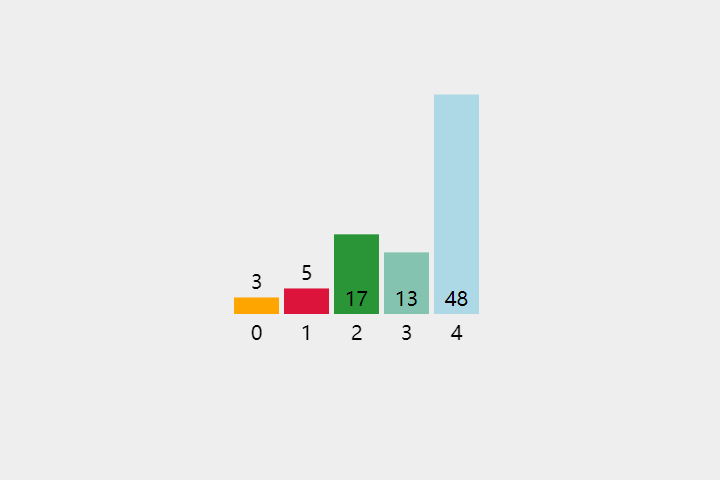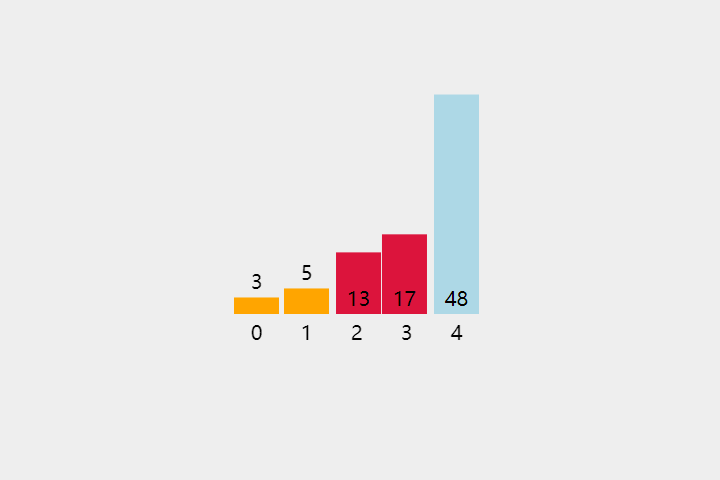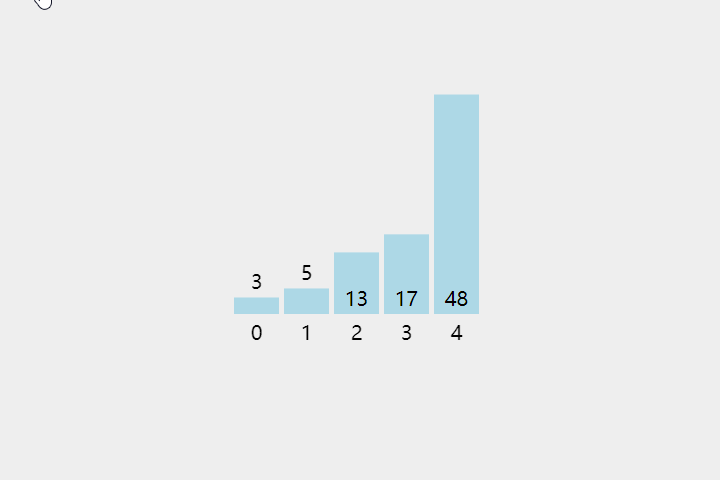
代码模板
public void selectionSort(int[] array) {
if (array == null || array.length == 0) {
return;
}
int n = array.length;
for (int i = 0; i < n - 1; i++) {
// 找到从 i 到 n-1 中最小的元素的索引
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
// 将找到的最小元素交换到当前位置 i
int temp = array[minIndex];
array[minIndex] = array[i];
array[i] = temp;
}
}插入排序
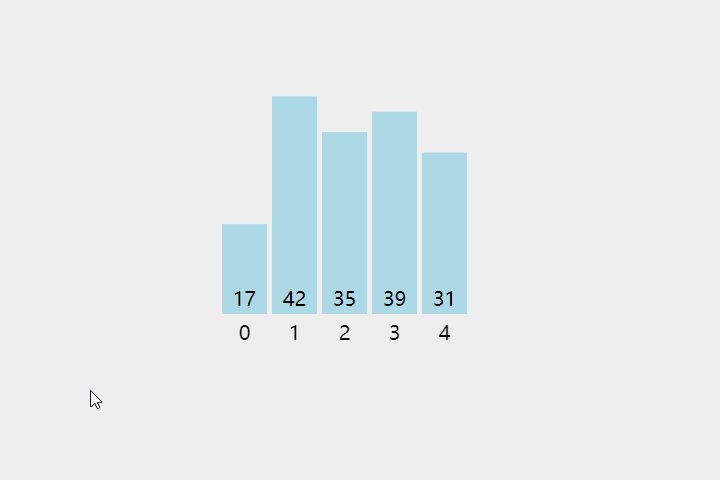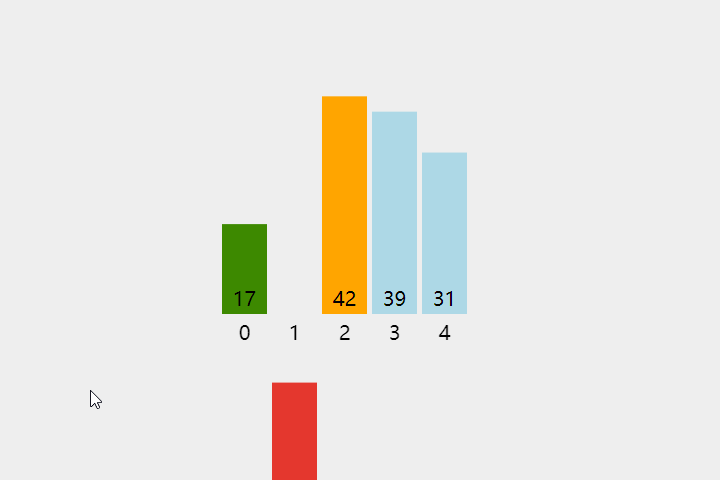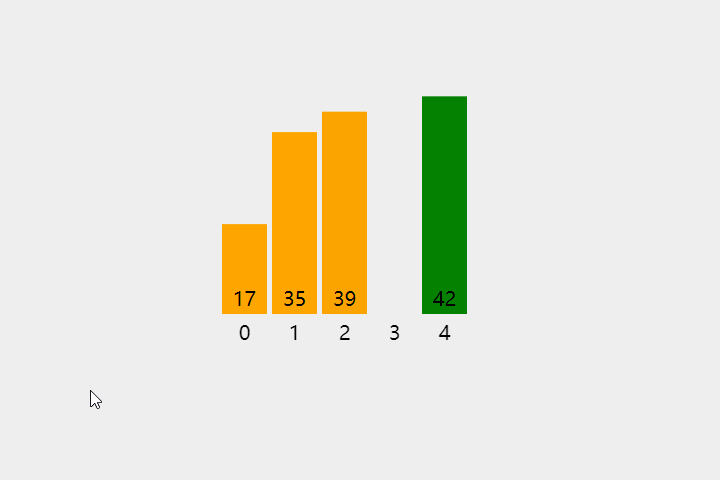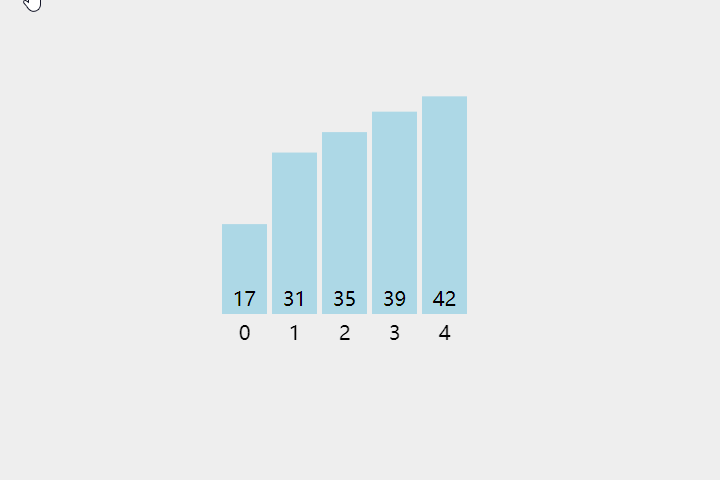
通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
算法步骤:
- 将第一个元素标记为已排序
- 对于每一个未排序的元素 X,位置设为 i
- 从
j = i - 1的位置开始「从后向前」扫描,如果不满足条件j >= 0 && array[j] > current - 就将未排序元素插入到
j+1位置中。
代码模板
public static void insertionSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
// 从第二个元素开始遍历,因为第一个元素可以认为是已排序的
for (int i = 1; i < array.length; i++) {
int current = array[i];
int j = i - 1;
// 将当前元素与已排序部分的元素比较,找到合适的位置插入
while (j >= 0 && array[j] > current) {
array[j + 1] = array[j];
j--;
}
// 插入当前元素到找到的位置
array[j + 1] = current;
}
}✨希尔排序
希尔排序是插入排序的一种优化版本
希尔排序的基本思想是将原始数据分成多个子序列,这些子序列的元素间隔相同,然后对每个子序列进行插入排序。随着增量逐渐减小,子序列的长度逐渐增加,直到增量为1,此时整个数组成为一个子序列,算法退化为普通的插入排序。
public static void shellSort(int[] array){
int len = array.length;
int temp, gap = len / 2; // 初始增量
while (gap > 0) {
for (int i = gap; i < len; i++) {
temp = array[i];
int preIndex = i - gap;
// 在子序列进行插入排序
while (preIndex >= 0 && array[preIndex] > temp) {
array[preIndex + gap] = array[preIndex];
preIndex -= gap;
}
array[preIndex + gap] = temp;
}
gap /= 2;
}
}✨归并排序
采用分而治之的思想,将数组分成两半,分别对这两半进行排序,然后将排序好的两半合并在一起。
// 归并排序的主函数
public void mergeSort(int[] array, int left, int right) {
if (left < right) {
// 找到中间索引
int middle = left + (right - left) / 2;
// 分别对左右两半进行排序
mergeSort(array, left, middle);
mergeSort(array, middle + 1, right);
// 合并排序好的两半
merge(array, left, middle, right);
}
}
private static void merge(int[] array, int left, int middle, int right) {
// 临时数组,用于存放合并后的有序元素
int[] temp = new int[right - left + 1];
int i = left; // 左半部分的起始索引
int j = middle + 1; // 右半部分的起始索引
int k = 0; // 临时数组的索引
// 合并过程
while (i <= middle && j <= right) {
if (array[i] <= array[j]) {
temp[k++] = array[i++];
} else {
temp[k++] = array[j++];
}
}
// 复制左半部分剩余的元素
while (i <= middle) {
temp[k++] = array[i++];
}
// 复制右半部分剩余的元素
while (j <= right) {
temp[k++] = array[j++];
}
// 将临时数组中的元素复制回原数组
for (i = left, k = 0; i <= right; i++, k++) {
array[i] = temp[k];
}
}✨快速排序
快速排序,和二分查找的思想很像,都是先将数据一份为二然后再逐个处理。
// 主函数,对数组array从index left到index right的部分进行快速排序
public void quickSort(int[] array, int left, int right) {
if (left < right) {
// 找到分区的索引
int partitionIndex = partition(array, left, right);
// 对左边的子数组进行快速排序
quickSort(array, left, partitionIndex - 1);
// 对右边的子数组进行快速排序
quickSort(array, partitionIndex + 1, right);
}
}
// 进行分区操作的函数
private int partition(int[] array, int left, int right) {
// 选择最右侧的元素作为基准值(pivot)
int pivot = array[right];
int i = (left - 1); // i用来记录比基准值小的区域的最后一个元素的索引
for (int j = left; j < right; j++) {
// 如果当前元素小于或等于pivot
if (array[j] <= pivot) {
i++;
// 交换array[i]和array[j]
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
// 交换pivot到它最终的位置
int temp = array[i + 1];
array[i + 1] = array[right];
array[right] = temp;
return i + 1;
}✨堆排序
而根据排序的方向又分为大顶堆和小顶堆:
- 大顶堆:每个节点值都大于或等于子节点的值,在堆排序中用做升序排序。
- 小顶堆:每个节点值都小于或等于子节点的值,在堆排序中用做降序排序。
/**
* 堆排序
* @param array
*/
public static int[] heapSort(int[] array){
int size = array.length;
// 先将数据放入堆中
for (int i = (int) Math.floor(size / 2); i >= 0; i--) {
heapTopMove(array, i, size);
}
// 堆顶位置调整
for(int i = size - 1; i > 0; i--) {
swapNum(array, 0, i);
size--;
heapTopMove(array, 0,size);
}
return array;
}
/**
* 堆顶位置维护
* @param array
* @param i
* @param size
*/
public static void heapTopMove(int[] array,int i,int size){
int left = 2 * i + 1;
int right = 2 * i + 2;
int largest = i;
if (left < size && array[left] > array[largest]) {
largest = left;
}
if (right < size && array[right] > array[largest]) {
largest = right;
}
if (largest != i) {
swapNum(array, i, largest);
heapTopMove(array, largest, size);
}
}
/**
* 比较交换
* @param array
* @param left
* @param right
*/
public static void swapNum(int[] array,int left,int right){
int temp = array[left];
array[left] = array[right];
array[right] = temp;
}计数排序
将数据转化为键存储在额外的数组空间里。
- 找出待排序数组中最大和最小的元素
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项
- 然后反向输出
/**
* 计数排序
* @param array
*/
public static void countSort(int[] array){
int bucketLen = getMaxValue(array) + 1;
int[] bucket = new int[bucketLen];
// 统计每个值出现的次数
for (int value : array) {
bucket[value]++;
}
// 反向填充数组
int sortedIndex = 0;
for (int j = 0; j < bucketLen; j++) {
while (bucket[j] > 0) {
array[sortedIndex++] = j;
bucket[j]--;
}
}
}
/**
* 获取最大值
* @param arr
* @return
*/
private static int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (maxValue < value) {
maxValue = value;
}
}
return maxValue;
}桶排序
桶排序算是计数排序的一个加强版,它利用特定函数的映射关系,将属于一定范围内的数据,放到一个桶里,然后对每个桶中的数据进行排序,最后再将排序好的数据拼接起来。
- 设置一个合适长度的数组作为空桶
- 遍历数据,将数据都放到指定的桶中,分布的越均匀越好;
- 对每个非空的桶里的数据进行排序;
- 将每个桶中排序好的数据拼接在一起。
/**
* 桶排序
* @param arr
* @param bucketSize
* @return
*/
private static int[] bucketSort(int[] arr, int bucketSize){
if (arr.length == 0) {
return arr;
}
int minValue = arr[0];
int maxValue = arr[0];
// 计算出最大值和最小值
for (int value : arr) {
if (value < minValue) {
minValue = value;
} else if (value > maxValue) {
maxValue = value;
}
}
// 根据桶的长度以及数据的最大值和最小值,计算出桶的数量
int bucketCount = (int) Math.floor((maxValue - minValue) / bucketSize) + 1;
int[][] buckets = new int[bucketCount][0];
// 利用映射函数将数据分配到各个桶中
for (int i = 0; i < arr.length; i++) {
int index = (int) Math.floor((arr[i] - minValue) / bucketSize);
// 将数据填充到指定的桶中
buckets[index] = appendBucket(buckets[index], arr[i]);
}
int arrIndex = 0;
for (int[] bucket : buckets) {
if (bucket.length <= 0) {
continue;
}
// 对每个桶进行排序,这里使用了插入排序
InsertSort.insertSort(bucket);
for (int value : bucket) {
arr[arrIndex++] = value;
}
}
return arr;
}
/**
* 扩容,并追加数据
*
* @param array
* @param value
*/
private static int[] appendBucket(int[] array, int value) {
array = Arrays.copyOf(array, array.length + 1);
array[array.length - 1] = value;
return array;
}基数排序
将整数按位拆分成不同的数字,然后再按照位数排序,先按低位排序,进行收集,再按高位排序,再进行收集,直到最高位。
/**
* 基数排序
* @param array
*/
public static void radixSort(int[] array){
// 获取最高位
int maxDigit = getMaxDigit(array);
int mod = 10;
int dev = 1;
for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
// 考虑负数的情况,这里扩展一倍队列数,其中 [0-9]对应负数,[10-19]对应正数 (bucket + 10)
int[][] counter = new int[mod * 2][0];
// 计数排序
for (int j = 0; j < array.length; j++) {
int bucket = ((array[j] % mod) / dev) + mod;
counter[bucket] = appendBucket(counter[bucket], array[j]);
}
// 反向填充数组
int pos = 0;
for (int[] bucket : counter) {
for (int value : bucket) {
array[pos++] = value;
}
}
}
}
/**
* 获取最高位数
*/
private static int getMaxDigit(int[] arr) {
int maxValue = getMaxValue(arr);
return getNumLength(maxValue);
}
/**
* 获取最大值
* @param arr
* @return
*/
private static int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (maxValue < value) {
maxValue = value;
}
}
return maxValue;
}
/**
* 获取整数的位数
* @param num
* @return
*/
protected static int getNumLength(long num) {
if (num == 0) {
return 1;
}
int lenght = 0;
for (long temp = num; temp != 0; temp /= 10) {
lenght++;
}
return lenght;
}
/**
* 扩容,并追加数据
*
* @param array
* @param value
*/
private static int[] appendBucket(int[] array, int value) {
array = Arrays.copyOf(array, array.length + 1);
array[array.length - 1] = value;
return array;
}